石塚正英
はじめに
今から10年程以前になるが、『科学するこころを開くScience Window』（2015年冬号）という雑誌で特集記事「なぜ数学を学ぶの？」を読んだ。その冒頭に、「秋山仁さんが語る『数学と歩む人生』」という記事があった。本誌を手にした私の関心は「なぜ学ぶの？」にあった。その問いは学ぶ理由や目的に関連しているが、秋山の答えには①外在的な事柄と、②内在的な事柄があった。①は平たく言うと、○○のために役だつ、ということを意味しており、「不可能を可能にし」、「合理的な生活を送るために」（7頁）という箇所がそれを象徴している。それに対して②は克己心や自己確証を意味しており、「自分の力でわかるようになる」（8頁）や「これが楽しくてしょうがない」（9頁）という一文がそれを象徴している（☆01）。この両面は機械的にすっきり区分できるわけでなく、また何も数学に限ったことではないが、私としてはあらゆる学問のうちで最も理論的抽象度の高い数学においてこそ、「なぜ学ぶの？」という問いかけを吟味したいのである。結論的な言辞を立てると、ピタゴラス以来、数学はソクラテス哲学と並んで超自然的な領域に絡んでおり、私にとってそこが眼の付けどころなのである。自然紋様（モノ）から抽出される幾何紋様（コト）は、翻って――つまり本末転倒して――（☆02）、自然紋様（モノ）を規定し説明する。たとえば、丸いモノは丸いコトを抽出し、翻って、丸いコトは丸いモノの基準となる。
さて、科学において①は自然（モノ）世界や生活世界に係るが、②は観念世界や理論（コト）世界に関わり、両者は相互に橋渡しが困難である。あえて橋渡し役を考えるならば、技術がそれに相当する。数学は理論であって技術ではない。秋山は言う。「私たちが目にし、実際に恩恵に浴することもある医療機器のほとんどに数学の理論が応用されています」（7頁）。数学は〔必要は発明の母〕に馴染まない。なぜなら、それは①にかかわるのであって、アルキメデスやコペルニクス、ニュートンたちの数学への熱意は、圧倒的に②から生まれているからである。彼らのインスピレーションは時代をはるかに飛び越えている。『数学をつくった人びと』の著者エリック・テンペル・ベルは言う。「古代最大の知性であるアルキメデスは、骨の髄まで近代的である。そしてアルキメデスとニュートンは、たがいに完全に理解しあえたであろう」（☆03）。だが、よくよく観察するならば、彼らの業績は時代の刻印を帯びている。その問題について、本稿では、フランス革命の残響が時代の行く末を予言していた1830年前後に活躍した数学者、エヴァリスト・ガロア（1811-32）を検討の対象とする。彼にとって数学という学問はいったい何だったのか。その問題を検討するに際して、同時代ヘッセンの医学志望者ゲオルク・ビュヒナー（1813-37）を比較の素材にする。
なお、本稿を執筆している最中の2025年3月26日、ノルウェー科学文学アカデミーは2025年度の「アーベル賞」（数学のノーベル賞と讃えられる）を日本の柏原正樹に贈ると発表した。「誰も想像しなかった方法で驚くべき定理を証明してきた」ことを授賞理由にしている。ガロアと同時代に代数方程式論や楕円関数論などに取り組んだノルウェーのニールス・アーベル（1802-29）もまた、②における数学者の一人だった。
一、1830年前後のフランス思想界
まずは、ガロアの思想と行動に深く影響を及ぼした1830年前後のフランス、パリについて概観する。それは政治的という以上に、革命的な雰囲気に染まっていた。具体的にはサン=シモン主義者とバブーフ主義者の隆盛である。
第一にサン=シモン主義者であるが、彼らは1825年の師サン=シモン没後、弟子のバルテルミ=プロスペル・アンファンタンとカルボナリ党出身のサン=アルマン・バザールを中心に活動していた。彼らは、師の教説とりわけ没年に刊行された『新キリスト教』を宣伝するため、1828年-29年に『サン=シモン学説解義』を出版した。その中には、カトリックとは縁遠い汎神論的な「新しい宗教」が説かれていた。これを拠所にして自由主義を含めた旧来の政治思想すべてを批判した。とくに市民的な所有権・相続制度を否定し、漸次的に進行する未来共同社会（アソシアシオン）への改革を主張したのである。この時期のフランス思想について、その頃パリに留学していたドイツ（シュレスヴィヒ公国）の法学者ローレンツ・シュタインは、著作『今日のフランスにおける社会主義と共産主義』（1842年）で、次のように記している。文中に記されているミシェル・シュヴァリエは、ガロアの親友オーギュスト・シュヴァリエの実兄である。
バザールは、彼の叛逆者集団の中ですでに力強く大胆な演説家としての名声を博していたが、いままた首都の公けの生活の中で自分の考えを述べる講義を開こうとした。（中略）そしてサン=シモン派は一つの重要な現象になり始めた。この時期に若い人たちが従い、のちにその一部は、周知の名声を博することとなった。カルノー、ミシェル・シュヴァリエ、デュジェ、バローの名前だけ挙げておこう。彼らには、共通の効果的で活発な努力があった。現代は彼らの誰にとっても満足のゆくものではなかったから、ぜひ将来を自分たちの理想に合うように作ろうとした（☆04）。
次にバブーフ主義者であるが、それはルイ・オーギュスト・ブランキの名と結びついている。彼は、七月革命（1830年）を機にフランスへもどってきたバブーフ主義者ブォナローティの思想的影響下でカルボナリ運動に加わり、共和主義から共産主義に転向する。フィリポ・ブォナローティは『平等をめざす、バブーフの陰謀』（ブリュッセル、1828年）でこう証言していた。フランス革命の渦中で「暫定的な革命権力機関に既存政府を置き換える計画が生まれた」。「第一の提案は国民公会の一部を再招集しようという案であり、第二のものは独裁体制（dictature）を設けようというもの、そして最後の提案は、革命を首尾よく達成する責任を担う新たな機関（corps）を設立しようというものであった」。結果は、ジャコバン的な唯一者による独裁でなく、ややサン・キュロット的な「少人数で構成される機関（corps peu nombreux）の方を選んだ」。いわば、妥協の産物だった（☆05）。
ブォナローティも、独裁は複数者によるものと結論したが、バブーフ処刑（1797年）の後ただ一人生き残り亡命していた段階で、必要悪としての集団的独裁という傾向を後退させ、積極的な少数独裁論を打ち出していた。やがて七月革命後のパリに帰還し、革命の元老としてブランキらの前に姿を現した。ブランキは、バブーフ的な意味の独裁、つまり集団的独裁をイメージするよりも、ブォナローティゆずりの個人的独裁に惹きつけられ、これに直接影響された。そのブランキは1830年代初期において、ルイ=フィリップの七月政体を特権市民の君臨する体制と規定した。さらには、それをサン・キュロットら労働民衆に立脚して転覆すべきと判断し、すすんで共和主義的急進運動の先頭に立った。すなわちブランキは、共和主義者の合法組織「人民の友協会(Société des Amis du people)」とこれにつづく「人権協会(Société droits du peuple et du citoyen)」に加わり反政府宣伝・示威行動に出、1830年代半ばになると共産主義の立場を明確にして秘密結社「四季協会(Société des Saisons)」を創設、武装蜂起を準備するようになる（☆06）。一連の系譜を持ったそれらの秘密結社のうち、ガロアは人民の友協会に加入していくのである。
ここでしばしガロアを離れ、同時代のドイツ（ヘッセン）でガロアと似たような生涯を送った青年ゲオルク・ビュヒナーの思想と行動に関する説明を指し挟む。1813年10月、ヘッセン大公国の首都ダルムシュタット近郊に生まれた彼は、12歳で同市のギムナジウムへ入学する。そして1831年にそこを卒業し、フランス（アルサス州）のストラスブール（シュトラースブルク）に留学し医学を学ぶ。アルサスとロレーヌ、またはエルザスとロートリンゲンというように、この地方は、ある時はフランス領に、またある時はドイツ領にされるという悲運な土地だった。その地でビュヒナーは二度にわたる革命の余韻を残すフランスを体験した。サン=シモン主義者の思想と行動がビュヒナーを捉える。ストラスブールにはやがてブランキらが指導する人権協会の支部が設立されていく。1831年から33年にかけての同地での生活は、ビュヒナーにとって貴重なものとなった。1833年4月にフランクフルトで抵抗運動が発生した。衛兵本部と警察本部を襲撃したのである。その事件を知ったビュヒナーは、数日後に家族に宛てて手紙を書いた。（ ）は引用者の記入（以下同様）。
今日、フランクフルトの事件に関する手紙を受けとりました。私の考えはこうです。もしこんにち何か役に立つものがあるとすれば、それは暴力です。（中略）若者たちは暴力をふるうといっては非難されます。けれども私たちは永久に暴力支配に釘づけされてはいないでしょうか。私たちは牢獄に生まれ育ってきたから、手足をがんじがらめにされて穴蔵におしこめられ、猿ぐつわをはめられているのに気づかないのです。いったい合法状態とは何のことでしょうか。何の値うちもない堕落した少数者の不自然な欲求を満足させるために、国家市民の大多数を苦役用の家畜にしたてる法律のことでしょうか。この法律ときたら、野蛮な軍隊の暴力とその法律の手先の愚劣さきわまる狡猾行為によって支えられているのです。この法律は、正義と健全な理性に加えられた際限なき、野蛮な暴力です。私はかなう限り、これに対して口と手で戦います（☆07）。
フランスでの思想的影響下で特権市民王政の諸矛盾を体験しつつあったビュヒナーにとって、革命指向は本能的ともいえるほどすさまじい。1835-36年当時、戯曲『ダントンの死』、小説『レンツ』などを書き下ろしつつ、彼は、ヘッセンの貧農たちの解放は革命を除いてありえない、議会や法律にかなった運動などごまかしでしかない、と考えていく。ただし、彼は革命の必要性を強調するとともに、そのような行動だけではけっして大衆は決起しないとも考える。この点は非常に重要である。だが少数者の死闘にかえて、何を提起しようというのか。そのあたりの含みは、革命の暴力を肯定する同時代人ガロアにも言い当たる（☆08）。ビュヒナーとガロアは、近代的法思想が伝統的慣習法を打ち砕いていく過渡期を生きた同時代人だったのである。
二、ガロア、二十歳の自己革命
エヴァリスト・ガロアの生涯を綴った幾つかの書物（邦訳）には、以下のような副題がついている。「その真実の生涯」、「神々の愛でし人」、「天才と狂気」、「天才数学者」、「革命家にして数学者」。私ならば「人はなぜ学問するか？」としたい。王立のリセ（教育機関）、ルイ=ル=グラン中学校時代の1827年、ガロアは授業の中で数学者ルジャンドルの著作『幾何学原論』を読んだ。その印象をポーランド出身の研究者レオポルト・インフェルトは著作『ガロアの生涯―神々の愛でし人』で次のように記している。「／」は段落、下線は引用者による（以下同様）。
ルジャンドルの著書を開いてはじめて予習をしかけたエヴァリストは、最初の数行を読みだした。（中略）「公理とは、自明なる（self-evident）命題である」。／彼は考える。「自明とは何だろうか？ ある人には自明であることでも、他の人にとっては自明でないかも知れない。誰にとってもつねに自明であるほど、十分に自明であるようなものが存在するだろうか？」彼は読み続ける。／定理とは、証明（demonstration）と呼ばれる推理によって明瞭となるところの真理である。／彼は考える。「とすると、幾何学は真理を扱うものなんだな。真であるところの定理が存在する」。（中略）／ページを追うにしたがって、幾何学の建築がギリシア神殿のような単純さと美しさで建立されてゆくのを、エヴァリストは眼のあたりにした。（中略）そして幾何学の抽象的な諸定理が、物質の世界よりももっと現実的なものとなった。彼の頭脳の中で、幾何学建築は完成してゆく。定理を読んでいると、ほとんどいつもほとんど一瞬間で、彼にはその証明方法がひらめくのだ。だからあとはあわただしく本文と作図とを眺めてみて、自分の考えがあっているかどうか確かめるだけだった。／まもなく彼は、証明の部を省くことができた（☆09）。
この時点において、ガロアの数学は技術のためでなく学問（科学）のために存在しており、②内在的な事柄となっていた。「幾何学の抽象的な諸定理」がそれを物語っている。対して、比較のために記されている「物質の世界」は①外在的な事柄に関わっている。こうした分析は私のオリジナルだが、人はなぜ学問するか、という議論には欠かせない区分である。それというのも、1830年7月27日、七月革命勃発の２日前にガロアが発した言葉に、②から①への転変といったニュアンスが浮上しているからである。なお、伝記でその件を記したインフェルトの書き方は目撃的叙述といって、インフェルトが当事者たちの眼前に臨んでいるかのように綴られている。つまり創作の手が入っているのである。その叙述スタイルを「創作的ロマン」として斥ける向きもあろうが、私は、大枠・大筋で研究資料と見なせる根拠を持つと思っている（☆10）。その点を考慮しつつ、以下にインフェルトから引用する。まずはサン=シモンの弟子ミシェル・シュヴァリエの弟オーギュストが口火を切る。
7月25日の日曜日に、オーギュスト・シュヴァリエとエヴァリスト・ガロアとは、リュクサンブール公園に腰を下ろしていた。数学のゼミナールでいっしょになってから、二人はよく午後の余暇をともに過ごしてきた。（中略）「ねぇ君、政治や社会の問題になると、ぼくは兄貴と同意見なんだ。ぼくの兄はね、いままでずいぶんぼくを感化してきたものだ。兄はサン=シモン伯爵の弟子の一人でね。君はサン=シモンのことを聞いたことがあるかい？」／「あまりないよ。聞かせてくれたまえ。」／「ぼくが科学、とくに数学を讃美するようになったのは、サン=シモンと兄のおかげさ」／「と言うと？ サン=シモンと数学とはどんな関係があるんだい？」／「サン=シモンが著わした最初の本を見れば、それがわかるよ。『ジュネーブ住人の同時代人に宛てたる書簡集』を読んでみたまえ」。（☆11）。
この時点からガロアの数学は革命のために、つまり①外在的な事柄となっていった。革命に向けた、革命のための数学である。サン=シモン（1760-1825）は、パリに生まれ、貴族の出身であったにもかかわらず、若くしてアメリカ独立戦争に参加した。帰国後フランス国内を旅行し、その間に、社会悪の根原が財産所有の不平等と貧困にあると判断し、新しい社会の建設を主張し始めた。彼は未だ労資の対立というものをさほど意識せず、大きく働く者と働かない者、利益をもたらす者とそれに寄生する者の2階級に分類を行う。その際、前者は産業者と称し、農民、職人などの勤労層に加え、商人、銀行家、資本家、科学者もこれに含まれる。また後者は有閑者と称し、地主、貴族、大金持、軍人などがこれに含まれる。サン=シモンによれば新しい社会は、前者が後者に代わって政権を担当し、産業者が自由に活動できるような社会である。そこでは、従来のような民衆を支配する道具としての国家は消滅し、産業者による富の生産とその自主管理をコントロールするような機関が残されるのみである。だが彼は、こうした新たな社会を導く手段としては､革命的な方法でなく、産業の指導者（科学者、技術者など）の改革に期待を寄せた（☆12）。
ところが、ガロアはシュヴァリエが勧誘するサン=シモン主義を遠ざける。彼はビュヒナーと同じような革命観を抱くに至ったのである。それを、インフェルトからの引用で確認してみたい。先ほどの引用に続く部分である。
ガロアが何も知らないので、シュヴァリエは驚いてしまった。だが、彼は根気よく説明してやった。（中略）／「愛が世界を征服し、憎悪が終焉することを我々は信じている。競争は存在しなくなり、世襲財産や戦争もなくなってしまうんだ。人類すべてに対する同胞愛が勝利し、新キリスト教が確立されるだろう、という信条さ」。（中略）／「ふん、愛という言葉は美しく聞こえるよ。しかし憎悪が爆発して、世界の土台石を揺さぶった後でなけりゃ、愛の支配なんてありえないよ。旧世界の廃墟の上にのみ、愛が育ちうるんだ。しかも旧世界を破壊しうるのは憎悪（hatred）だけだ。大革命はその破壊に成功しなかった。人々はまたきっと革命をやり直さなきゃならないんだ」。（中略）／「死体が人々を叛乱に決起させるとわかっていれば、ぼくはすすんで自分の死体を差し出すよ（If I knew that a corpse would stir the people to revolt I would give them mine.）」（☆13）。
ガロアは数学論文を数度にわたって科学アカデミーに提出したが、いずれも採用されず掲載に至らなかった。本人としては何らかの憶測・邪推を抱いてしまうのだった。そのせいでガロアは政治的に急進化した、その根拠は度重なる不運にあったというような説明が、ガロアの伝記で書かれる。私としては、それを完全否定するつもりはない（☆14）。けれども、およそ数学研究で人生を展望していたガロアにとって、もっとも重要なのは机上における数学の錬成である。それを阻害する要因除去としての現状転覆なのである。対人関係における疑心暗鬼や猜疑心、自暴自棄だけから革命結社に加わったのではない。1789年に開始したフランス革命のさらなる進行をガロアは望んだのである。その意味では、徹底的な破壊こそがすべての突破口である、と考える19世紀ドイツの革命職人ヴィルヘルム・ヴァイトリングやロシアの革命家ミハイル・バクーニンと共通する反抗心を養っていたのだろう（☆15）。研究熱心であればあるほど、時代への反抗意識は高揚する。数学という文化の領域めがけて政治の領域から潰しにかかる勢力への反撃を企てたのである。1811年生れのガロアの、①と②とを股にかけた〔二十歳の自己革命〕だったと言える（☆16）。
三、数学というメソフィジカルな学問
さて、本稿の主要な論題は、ガロア論でなく学問論である。インフェルトのガロア伝記を読んでいると、①外在的よりも②内在的の方が多く出てくる。すでに幾箇所かは引用済みだが、さらに必要箇所を引用する。
数え年で17歳になったガロアは、数学上の大発見をしたと自分で思いこんでいた。重大問題が解けた、すべての五次方程式は羃根（累乗根）によって解けるという証明ができた、と彼は信じたのである。しかし後になって、自分の証明を何度も検討しているとき、推理を間違えていたと明瞭にわかる瞬間がきた。何カ月も執拗に苦闘して得た発見が崩れ去って、意味のない記号の堆積にすぎなくなってしまったのだ。しかし彼はひるまなかった（But he did not give up;）。偉大な科学者のすべてがつねにわきまえていたように、彼もまた知っていた。絶え間なく遮二無二思索を進めてこそ、はじめて一縷の光明がやってくるのだということを（☆17）。
なぜ学ぶの？ 好奇心？ 繰り返すが、その問いは理由や目的に関連している。答えには①外在的な事柄と、②内在的な事柄とがある。①は平たく言うと、○○のために役だつ、ということを意味している。それに対して②は克己心や自己確証を意味している。インフェルトにしたがうならば、ここでのガロアは明らかに②の数学者だ。
ただし、上記引用文中に記されている「数学上の大発見（a great discovery）」は、「大発明（a great invention）」と評価するのが適切である。理論上で新たな境地を創出ないし構築するからである。たとえばアインシュタインとの共著『物理学は如何に創られたか』において、インフェルトは「微分法の発見（the discovery of differential calculus）」という表現を用いているが（☆18）、それも正確でない。微分法など、いわゆる定理は、化石や遺物のように前以って埋もれていたものが発見される類のものではなく、新たに発明されたり考案されたり、確立したりする類のものである。そうした定理は数学的存在（観念）であって、曲線など現実的な象形や現象（物質的存在）を前提に創出されるメソフィジカルな特徴を有している。この言い回しはインフェルトのものなのか、その点は不明であるが。
さて、ガロアはどうだろうか。彼が明らかに②の数学者だと判断できる、その決定的な言葉が次の引用文に綴られている。
（1831年1月13日の自主講義において）彼は練りに練った講義を始めた。／「人間の持つすべての知識のうち、数学は最も抽象的で最も理論的なものであり、我々の感覚印象の世界に訴えることのない唯一のものであります（mathematics is the most abstract, the most logical, the only one which does not appeal to the world of our sense impressions.）」（☆19）。
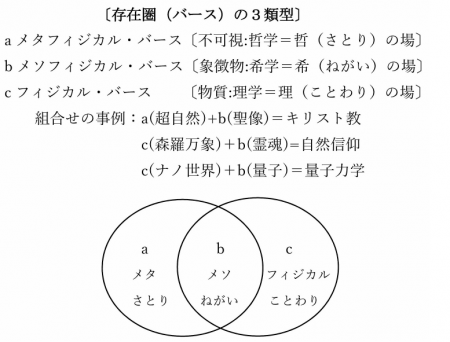ガロアが②の数学者だという、その意味内容は、私のオリジナルである〔メソフィジカル・バース〕の定義にぴったり当てはまる。私は、現実世界と観念世界の総体を概観する目的で、自然世界をベースとする3層の存在圏を想定し、〔存在圏（バース）の３類型〕と命名している。よく知られているのは下層「自然世界（フィジカル・バース）」と上層「超自然世界（メタフィジカル・バース）」である。その中間に、どちらともつかない中層の「中間世界（メソフィジカル・バース）」をおくのである。上層（a）は不可視であり、プラトンのイデアやキリスト教の神の存在圏である。哲学＝哲（さとり）の場でもある。下層（c）は可視であり、ニュートン力学で説明される圏域であり、理学＝理（ことわり）の場でもある。そして中層（b）は、森羅万象のいずれかに霊魂や神霊、精霊が潜む自然信仰・民間信仰の存在圏で、希（ねがい）の場でもある。ガロアの言う「我々の感覚印象の世界に訴えることのない」圏域・純粋数学的存在は、（c）数学者（人間世界）が作った観念世界なので（b）〔メソフィジカル・バース〕であり、21世紀における典型は量子世界（ナノ世界）である（☆20）。自然世界での運動・現象である光の速度は観察（数学）で求められる。しかし、量子世界（ナノ世界）での運動・現象である量子の振舞いは観察では求められない。自然世界には存在しない環境、数学的環境において確認できるのみである。ただし、量子力学が古典的力学の世界を駆逐する、などという愚論を思いつかない限り、すべては（c）フィジカル・バースから立ち上がる（☆21）。私にすれば、その確認こそ、数学が②内在的な学問に一致する根拠となっている。また、そのことはベルの次なる言葉によっても示唆される。とりわけ私が引いた下線部に注目して欲しい。
セレスは、数学にとって大きな災いであった。なぜガウスが、この星に夢中になったかを理解するには、死後すでに70年以上もたっていたニュートンの巨大な姿が、まだ1801年の数学界をおおっていたという事実を想いおこさなければならない。当時のいわゆる《大》数学者とは、ラプラスのように、天体力学のニュートン的建築を完成するために努力する人間のことをさしていた。数学はまだ、当時数理物理学、数理天文学と混同されていた。アルキメデスが、紀元前3世紀に心に描いていた、自立的科学としての数学の構想は、ニュートンの燦然たる光彩の中にその姿が見失われていた。数学が自己への奉仕を第一の義務とする科学であることがみとめられたのは、若いガウスが再びその構想をわがものとしてからのことであった（☆22）。
ベルが記している「自己への奉仕を第一の義務とする科学」こそ、本稿で私が強調する②内在的な学問と一致している。少なくとも、私にはそのように思われてならない。物理学や天文学との混同は、遠く古代エジプトやバビロニアに遡るが、その当時は「混同」という意識や概念すら曖昧模糊としていた。その限りで結論するならば、数学が観測や実験などの技術から分岐・自立して②内在化するのは近代に至ってからだろう。そのほかベルは、『数学をつくった人びと』の中で次のように記している。
自然科学者が、数学それ自身のための数学に無関心なのは、純粋数学者にとっては心外なことであるが、同様に純粋数学者がどっちでもいいようなギリシア文字イオタの添え書きを省略するのも、他の種類の衒学者にとっては心外なことであろう。その結果、科学にいちじるしい貢献をなし得た純粋数学者は、きわめて少数しかいなかったのである（☆23）。
ここに記されている「数学それ自身のための数学に無関心な」人は①タイプで、「純粋数学者」は②タイプである。18世紀まで理数系研究者の多くは大学よりも王立科学アカデミーに場を得ていた。フランス革命期に算数や数学を担当した教師は物理学（ラプラスなど）とか天文学（ラグランジュなど）とかと数学を兼務していた。彼らはそうした環境の中で数学をも研究していた（☆24）。その後19-20世紀に向かう過程で、科学における方法の研究（工学的技術革新）は①外在的な度合いを強め、論証ないし定理の証明（理学的基礎研究）は②内在的な研究として自立化をはかっていった。そうこうしているうちに、科学精神の基礎である「なぜそれが成り立つか？」が問われなくなっていった。その理由の一つを、ベルの次なる言葉が示唆している。「ライプニッツが（おそらくはニュートンも）正しい方法をみつけるまでに、多大の思考と度重なる試練とを要したことでも、現在では微積分学の初歩者の手でもやすやすと解くことができる」（☆25）。つまり、「なぜ？」という問いの答えは「自明の理」、「言わずもがな」と見なされてしまったからである。はたしてそうだろうか。
参考までに、私が高校時代（1965-1967）に数学の授業で教わったある初歩的な定理とその証明を、思いだしつつ例示する。〔定理〕「連続する 3つの整数の積は6の倍数である」。〔証明〕連続する 3 つの整数の積を f(n) = (n−1)n(n+1) とする。f(n) が 6 = 2 × 3 の倍数であることを示せばよい。そのためには、f(n)が2の倍数でもあり3の倍数でもあることを示せばよいことになる。連続する3つには必ず偶数が含まれるので、明らかにf(n)は2の倍数である。また、連続する3つには必ず3の倍数も含まれるので、明らかにf(n)は3の倍数である。したがってf(n)は6の倍数である。数学を学ぶということは、こうした証明の積み重ねを「自明の理」として必要とする。しかし、教育の現場では定理の暗記（語呂合わせ）が一般化している。たとえば、以下に示す三角関数における「正弦（sin）の加法定理」のように。sin(α±β)=sinαcosβ±cosαsinβ は「咲い(sin)たコス(cos)モス、コス(cos)モス咲い(sin)た」と覚える。これはその場しのぎの解答法であり点数稼ぎとしてはあり得ても、証明（単位円を利用するなど）を含む理解となってはいない。数学を公式暗記的に学んだ場合、②内面的動機はまず沸いてこない（☆26）。こうして「自明の理」は、知らなくてもいいことと誤解され、「無知の無知」（知らないことを知らない）を生んでしまったのである。
ガロアは、ルイ=ル=グラン在学中にルジャンドルの『幾何学原論』を読む。その時の模様を歴史学者ポール・デュピュイはこう記している。「彼はルジャンドルの“幾何学”を手にするやいなや、ほかの人が小説を読むような調子で端から端まで読んでしまった」（☆27）。また、研究者の加藤文元はこう記している。「ルジャンドルの『幾何学原論』が、十五歳の少年ガロアを一瞬のうちに数学に目覚めさせた。このこと自体には偶然はない」（☆28）。幾何図形はそのままで神々しく尊い。数学は論理的ではあっても合理的ではなく、現実世界から離れるにしたがい合理性は失われ、審美性（esthetics）が増幅していく。その圏域でガロアは、「数は宇宙を支配する」としたピタゴラス教団の原初的精神に触れあっていたのではないか、と私は連想する（☆29）。そのような経緯をもって、ガロアは、数学における②内在的な確証をインスパイヤーされたと思われる。直感的な学術的構想としての幾何学よりも、直観的な思想的洞察としてのそれに魅了されたのだろう。まさしく〔メソフィジカル・バース〕である。絵画でいえばシュールレアリスムだろう（☆30）。近代と理性を否定するシュールレアリスム（超現実主義）は観念（抽象）の一種ともいえるが、反面でそれは先史・野生に起因する象形（可視・具象）の反対物である。ガロアの「目覚め」は、その超現実観念（メタフィジカル）と象形（フィジカル）の中間（メソフィジカル）に生じたのだろう。
むすびに
私の持論であるが、学問を表現する図式として1970年以来、折に触れて次の図式を使う。学問＝〔知識･技術⇄思想〕（⇄は相互に影響を与え、交互的に支えあうことを意味する記号）（☆31）。知識と技術は、客体（自然･社会）に対する人間のかかわりに必要であり、それらの相互関係は、学問が科学として成立していく過程に反映されてきた。学問は、人間が自然･社会にかかわることを前提として、さらにはその結果として生まれ、発展してきたが故に、思想を内包する。思想なくして、また「かかわり」なくして、学問は必要とならなかった。そのことは、例えば物理学との関連では理論物理学（理論知）よりも実験物理学（技術知）に当てはまるだろうし、数学との関連では純粋数学よりも応用数学において指摘できる。
その際、純粋数学は自然とのダイレクトな関係が希薄である。虚数の概念など、その一例といえようか（☆32）。純粋数学は、経験や論理を前提とする「直感」よりも、非局所的で瞬時的な「直観」において冴えわたる。それはまさしくシュールな学問だ。ガロアの心中は、理屈なしにぴかっと閃いたはずである。天才とは1パーセントの霊感（inspiration）と99パーセントの発汗（perspiration）といったのはトーマス・エジソンだが、彼は数学者でなく技術者である。天才エジソンは、どちらかというと①外在的な発明家である。それに対して、天才ガロアは②内在的な発見者である。私は、私自身もそうありたいと願うのではあるが、②の使命を遂行するガロアの学問精神を最大に評価するものである。ベルは草創期の幾何学についてこう書いている。「いくつとなく幾何学が創られ徹底的に研究された。数学者がそれらを創った当時には、これらを何かの役に立てようという意図はなく、創造そのものへの興味からのことであった」（☆33）。これぞ②内在的動機の真骨頂ではないだろうか。
1832年5月30日、彼は恋愛のもつれ事に起因する決闘で負傷し、翌日に死ぬのだが、決闘の前日付で、親友のシュヴァリエに宛てて以下の書簡を送っていた。
「親愛なる友よ／ぼくは解析において若干の新発見をした」。／すぐその次から彼は数学に没入し、専門的なことを書き連ねる。この草稿が印刷されるかも知れない、そして数学者たちに読まれ討論され、批評され分析されるかも知れないのだ、と彼は意識しながら綿密に書き続ける（☆34）。
この時点で数学は、ガロアにとって紛れもなく②内在的な事柄となっていた。パラノイアを患っていたと指摘する人々もいるが、そうであろうとなかろうと、①外在的な事柄、すなわち革命のためというよりも、②内在的な行為すなわち数学をとおしての自己確証として学問する人ガロア、それが彼の生涯を表現するフレーズである。七月革命に共鳴するガロア、新国王ルイ=フィリップ暗殺の嫌疑をかけられサン・ペラジー牢獄に収監されるガロア、そのいずれの場面にあっても思念を数学に集中させる姿勢、それは彼が「学問がしたい！」という内在的使命感に支えられていたからこそ、我々は真に理解できるのである。そのあたりの描写としては、インフェルトに倣った目撃的叙述にまさる手法はないだろう。
注
01 「秋山仁さんが語る『数学と歩む人生』」、『科学するこころを開くScience Window』特集「なぜ数学を学ぶの？」2015年冬号（通巻57号）、JST（科学技術振興機構）、7頁、9頁。
02 「転倒」、これこそわが研究歴におけるキーワードである。詳しくは以下の拙著を参照。『価値転倒の社会哲学―ド=ブロスを基点に』社会評論社、2020年。
03 エリック・テンペル・ベル、田中勇／銀林浩訳『数学をつくった人びとI』早川書房、2003年、61頁。ちなみに、ベルは同書の21頁で19世紀ドイツの数学者レオポルト・クロネッカー（1823-91）の言葉を引いている。「神は整数を創りたもうた。残りすべては人間の業である（Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.）」。この言葉のうち、整数（die ganze Zahl）は、私ならば自然数（die natürliche Zahlen）に変更したいし、人間の業（das Menschenwerk）は数学だと思っている。ラテン語“mathematica”には「数学」のほかに「占星術」という意味がある。つまり前近代において、数学は占いの技術（道具）だったわけである。
04 ローレンツ・シュタイン、石川三義／石塚正英／柴田隆行訳『平等原理と社会主義―今日のフランスにおける社会主義と共産主義』法政大学出版局、1990年、226-227頁。
05 フィリップ・ブォナローティ、田中正人訳『平等をめざす、バブーフの陰謀』法政大学出版局、2020年、165頁、170頁。
06 石塚正英『三月前期の急進主義―青年ヘーゲル派と義人同盟に関する社会思想史的研究』長崎出版、1983年、第2章第2節、参照。
07 G. Büchner, Werke und Briefe, Gesamtausgabe, Leipzig 1968, S. 389.
08 1832年5月25日、エヴァリストはオーギュストに書き送っている。「ぼくは暴力を肯定する（I approve of violence）。頭ではできないとしても、ぼくの心情がそれを肯定する。ぼくはみずからの苦悩すべてに対して、復讐を遂げたいと願っている」。Leopold Infeld, Whom the Gods love, The Story of Evariste Galois, 1948. renewed New-York, 1975, p.274. レオポルト・インフェルト、市井三郎訳『ガロアの生涯―神々の愛でし人』日本評論社、2008年、333頁。
09 ibid., p.52-53. 邦訳、67-68頁。
10レオポルト・インフェルト（1898-1968）はポーランドの理論物理学者である。インフェルトはアルベルト・アインシュタインと親交を深め、共著『物理学はいかに創られたか』を刊行した。また、ケンブリッジでマックス・ボルンと量子力学の分野で交流した。ラッセル・アインシュタイン宣言の共同署名者であり、この宣言から生まれたパグウォッシュ会議の創始者でもあった。アインシュタインはインフェルトのガロア論を高く評価している。Cf. Helen Infeld, About the Auther, in; ibid., p.vii-ix.
なお、「目撃的叙述」とその効果について、私はジョン・ウィラー・ベネット、酒井三郎訳『悲劇の序幕―ミュンヘン協定と宥和政策』（日本出版サービス、1977年）で知った。文字どおり、叙述スタイルは目撃的というべきか劇作的というべきか、まさに悲劇（ナチス・ドイツのズデーテン進駐）への序幕としての事実経過（1938年9月下旬のミュンヘン会談）を、臨場感を添えて表現するスタイルをとっている。私は、記録の一スタイルとして意義を有していると思っている。研究者の佐々木力は、『ガロワ正伝―革命家にして数学者』（筑摩書房、2011年、25頁）において、インフェルトを意識しつつ自著の特徴を次のように記している。「創作的ロマン」ではなく「歴史学的批判に十分耐えうる史実の記述――それが、本書の歴史記述法のモットーである」（25頁）。「創作的ロマン」を超える「数学史的真実の提示を目標とするものである」（26頁）。むろん、その方が重要との指摘は当然である。けれども、インフェルトと交流のある訳者の市井三郎による以下の解説にも大いに賛同する（インフェルト、前掲邦訳、400頁）。
インフェルトによるその伝記は、ある意味で不思議な傑作であった。本文は小説風に書かれ、多くの会話や演説が「創作」されているのだが、巻末にはかなり長い「追記」が添えられており、どこまでが史料にもとづく真実であり、どこが数少ない史料と史料とを矛盾なくつなげる創造的推理であるかを、詳しく解説しているのだ。最後につけられた「文献解題」にいたっては、当時のフランスの歴史的状況を描くために、警視総監の回想記や、警察側のスパイの記録までがあげられている。この伝記を書くために、インフェルトは当時まで閲覧可能なあらゆる文献を、第二次大戦中にくわしく読破していたのである。その上で小説風に「読ませる」文体で書き上げたのだ。
11 Leopold Infeld, ibid., p.108-110. 邦訳、136-137頁。
12 サン=シモンのニュートン論については以下の文献を参照。中村秀一『産業と倫理――サン・シモンの社会組織思想』平凡社、1989年。同書には以下の記述が読まれる。「サン・シモンの初期の著作の前半部分は、『ニュートン教』という名称に象徴されるように、〈精神的権力〉の再組織のために、数学・物理学者を中心とした『科学的アトリエ』の再組織を構想していたと言ってよいであろう」100頁。
13 Leopold Infeld, ibid., p.108-110. 邦訳、135-137頁。
14 佐々木力、前掲書にはこう書かれている。「2月には科学アカデミー宛送付され、科学アカデミーの終身書記のフーリエが査読するはずであったが、彼は不幸にして、5月16日亡くなってっしまった。没後、遺された書類からガロワの論文は見いだされなかった」（76頁）。なお、エリック・テンペル・ベルは前掲書（306頁）において、急進化の原因を、この一件よりも以前のルイ=ル=グラン時代に見いだしている。
1823年12歳のとき、ガロアはパリのルイ・ルグラン高等中学校（リセ）に入学した。これがガロアのはじめての学校生活だった。その学校には、陰気くさい恐怖の空気がたちこめていた。（中略）学生たちは、校長がイェズス会士を学校にむかえようと企んでいるのではないかと疑ってストをやり、礼拝堂で賛美歌をうたうのを拒否したりした。校長は両親にも通告せずに、主犯とおぼしき学生を放校にした。ガロアはその仲間にははいらなかったが、放校されていたほうが彼のためにはよかったかもしれない。／それまで専制とは、この12歳の少年にとっては、単に言葉の上のことにすぎなかった。しかしいまや、ガロアは専制が生きながらえているのを目のあたりにみた。この経験が、生涯彼の性格の一面を形造る。彼の受けた衝撃は、なだめることのできない憤激へと変わった。
15 ヴァイトリング（1808-1871）やバクーニン（1814-1876）の総破壊思想については、以下の拙著を参照。『革命職人ヴァイトリング―コミューンからアソシエーションへ』社会評論社、2016年。
16 このあたりの文脈は、わが実存と重なり合っている。私は、1970年前後の全共闘運動の全盛期に大学生活を送った。浪人中に理系から文系に転向したものの、進学の動機は明確に「学問がしたい！」だった。ずっと後に、回想的に以下の文章を綴っている。「私は政治闘争をしに大学へやってきたのでなく、学問しにやってきたのです。浪人時代に最もやりたいと思っていたのは明治維新史、ロシア革命史、インド古代哲学思想、そして実存主義哲学でしたが、大学にきてからは唯物史観、ヨーロッパ労働運動史の研究にのめり込んでいきます。私にとって大学闘争は、あくまでも学問研究の自立空間を求めるがゆえの、生活上の営為だったのです」。『学問の使命と知の行動圏域』社会評論社、2019年、63頁。私は、ある意味では、〔学問と闘争〕というスタンスから本稿ガロア論の執筆を思い立った。
17 Leopold Infeld, ibid., p.63. 邦訳79頁。
18 Albert Einstein／Leopold Infeld, The Evolution of Physics――The Growth of Ideas from Early Concepts to Relativity and Quanta, New-York 1942, p.25. アインシュタイン・インフェルト『物理学はいかに創られたか―初期の観念から相対性理論および量子論への思想の発展』（上巻）岩波新書、2013年（初1939年）、27頁。
19 Leopold Infeld, ibid., p.169. 邦訳、205頁。なお、この点に関連する指摘として、佐々木力は前掲書で以下のように記している。「ほとんど例外なく、少年や少女が数学の学習に熱心に取り組むようになるのは、中等教育レヴェルですぐれた数学教師と出会うことによっている。その点は、 数学という人間をかなり超越したような学問もじつに人間的な学問であることに変わりはないのである」（59頁）。引用文中の下線は私が引いたものであるが、その意図は、数学こそメソフィジカルな学問だと思うからである。なお、ガロアの数学恩師はルイ・ポール・エーミール・リシャール（1795-1849）である。
20 〔存在圏の３類型〕に関する一層詳しい説明は、以下の拙稿を参照。「自然と超自然の緩衝域を考える」、石塚正英『原初性漂うハビトゥスの水脈―量子世界・地中海・ゲルマン・クルド』社会評論社、2024年、第2章。
21 アインシュタイン・インフェルト『物理学はいかに創られたか』には、量子力学によって古典力学が滅ぼされるような印象を与える見出しが読まれる。第1章が「力学的自然観の勃興」となっているのに対して、第2章は「力学的自然観の凋落」となっている。文脈上、凋落するのは自然観であって力学ではないものの、誤解の恐れなしとは言えない。私にすれば、地球という自然世界が存続する限り、古典力学的自然観とて量子力学によって凋落するとは思えない。Albert Einstein／Leopold Infeld, ibid., p.1, p.69. 前掲邦訳、3頁、79頁。
22 エリック・テンペル・ベル、前掲書II、79頁。
23 エリック・テンペル・ベル、前掲書I、383-384頁。
24 ジュール・ミシュレ、大野一道訳『民衆』みすず書房、1977年、276-277頁、参照。なお、ベル（同上、I、331頁）によると、ラグランジュはマリー・アントワネットの寵臣（数学教師）だった。
25 エリック・テンペル・ベル、前掲書I、249頁。
26 高校時代の私は、いわゆる理系を志望していたのだが、〔数学III〕で躓き、やがて興味が失せた。当時の数学教員が手抜きしていたのでなく、大学受験を意識した学習指導要領にしてからが、「なぜそうなるのか」よりも「どうすれば解けるのか」へと教育方針が偏っていたのである。つまり、私の区分における①外在的な傾向、当時の表現では〔産学共同〕の傾向を有していたのである。それとは別に、1965年3月、私は長野県の野尻湖でナウマンゾウ化石の第4次発掘調査団に参加した。今から振り返れば、湖畔にトレンチを掘ったりするフィールドワークに、私は②内在的な動機を感じていたのだろう。
27 ポール・デュピュイ、辻雄一訳『ガロア―その真実の生涯』東京図書、1972年、20頁。訳者あとがきに以下の記述が読まれる（157頁）。
本書は、パリ高等師範学校（エコール・ノルマル）の科学年報第3シリーズ第13巻（1896年）に発表されたP. デュピュイ（エコール・ノルマルの歴史学教授）の研究論文“エヴァリスト・ガロアの生涯”の全訳である。これは、ガロアという人物を研究したほとんど唯一のものだと言っても過言ではないほどの古典である。
28 加藤文元『ガロア―天才数学者の生涯』中央公論社、2010年、52頁。
29 エリック・テンペル・ベル、前掲書I、20頁。
なお、図学の専門家である堤浪夫は「図学の萌芽的研究」（『図学研究』第58号、武蔵野美術大学、1992年）の中で次のように記している（34頁）。
比例の中でa：b=b：a+bの黄金比について考えてみる。ピタゴラス教団の紋章は正五角星であるが、これは黄金比の結晶図形である。教団は数によって宇宙全体が造られていると信じていたけれども、黄金比には無理数√5を含むため、自然数しか知らなかった当時、己の教団の紋章を解明できなかった。それでいて美しい。西洋では魔除けになり、逆に健康のシンボルになっていった。ゲーテの「ファウスト」でも敷居に刻まれた正五角星が魔除けとして使われている。
30 石塚正英『バロック的叛逆の社会思想―ニーチェ・フロイト・ブルクハルト批判』社会評論社、2023年、第2章「野生的なまなざしの象形画家ジョアン・ミロ」参照。
31 石塚正英「学問論の構築へ向けて」（1970.12-71.02）、『学問の使命と知の行動圏域』、43頁、参照。
32 虚数について一言する。 i2= −1 （2乗して－1になる数、 x2=－1の解）を満たす想像上の数iを虚数単位といい、それを含む数を複素数（complex number）といい、虚数（imaginary number）ともいう。複素数zをz = a + bi（係数のa,bは実数）と表す。a を z の実部 （real part）、b を z の虚部 （imaginary part）という。そのうち、aのみがゼロの複素数を純虚数（pure imaginary number）といい、bのみがゼロの複素数を実数（real number）という。すなわち、複素数には純虚数と実数の２種類が存在する。
さて、問題は「虚数（imaginary number）」の語幹「虚（imaginary）」にある。直訳すれば「想数」となる。こちらの訳語からなら、少なくとも嘘は漂ってこない。実数としては存在しないが計算上では存在している。虚数という語の意味が分からない、ということと、虚数という語の意味は分かるが、それが示す対象がわからない、ということは別のことである。例えば「白いカラス」にあてはめると、白い色をしたカラスという意味はわかるが、そのような色をしたカラスは実在していないので、それが示すものがわからない、ということである。ただし、虚数の場合は、「2乗して－1になる数」と決めたのだから、その限りで誰もが想像上の存在を納得できる。それは数学の合理的な特徴である。その点で、量子（quantum）はまったく次元を異にする。これは人間が決めたものではなく発見されたものだからである。それがなぜ存在しているのか、なぜ不可解に動くのか、発見から100年経ても、誰も説明できていない。しかし、これとて数学的存在であるから、「発明」にも思える。素粒子の一つ、光の粒子である光子（photon）は、アインシュタインによって光量子（light quantum）と命名されもしたが、それは質量を持たない。紛れもなく数学（技術）によって発明された存在である。それよりなにより、発明の技術的道具である数学は、発見されたのでなく発明された人工的存在であり、それによって産出される世界もまた発明品だ。それらの発明品が置かれる場は〔メソフィジカル・バース〕である。
33 エリック・テンペル・ベル『数学は科学の女王にして奴隷I―天才数学者はいかに考えたか』早川書房、2004年、97頁。
34 Leopold Infeld, ibid., p.228. 邦訳、348頁。
【付記】わが学問論の構築は、上記の注31に記されている論説「学問論の構築へ向けて」を嚆矢としている。よって錬成歴は1970年-2025年になる。結果的ではあるが、私は〔自己確証〕として学問の道を歩んできたのだった。生きるために学問するのでなく、学問するために生きるのでもない。学問することが生きることなのである。世間ではよく、「文系の頭」とか「理系女（リケジョ）」とか区分けして、自らを誤認している人が多い。私の歩みは①理系（大学受験まで）→②文系（大学院まで）→③文理複合（理工学部に就職してから）と転変してきた。多様を味わって堪能でき、まずは楽しい半生である。健康寿命の続く限り、わが使命を淡々とまっとうしていきたいと念じている。
（いしづかまさひで）
(pubspace-x12955,2025.04.05)